
So if s is equal to negative 5, or s is equal to 7, then we have satisfied this equation. Solving Quadratic Equations by Factoring exercise State the solutions of the equation ( x + 6 ) ( x 1 ) 0 (x+6)(x-1)0 (x+6)(x1)0. Now we have to divide the two factors +6 and +9 by the coefficient of x 2, that is 2. That is one solution to the equation, or you can add 7 to both sides of that equation, and you get s is equal to 7. So, m ultiply the coefficient of x 2 and the constant term "+27".ĭecompose +54 into two factors such that the product of two factors is equal to +54 and the addition of two factors is equal to the coefficient of x, that is +15. So both of these satisfy that equation up there. Strategies: 1) Define your variables (Set-up the let statement). Solving quadratics by factoring: leading coefficient 1. You get x could also be equal to positive 5/2. Students will solve real-world applications that involve quadratic equations and factoring. Solve quadratic equations of the form ax2+bx+c0 that can be rewritten according to their linear factors. In the given quadratic equation, the coefficient of x 2 is not 1. You could get one solution is negative 5/2. In the given quadratic equation, the coefficient of x 2 is 1.ĭecompose the constant term +14 into two factors such that the product of the two factors is equal to +14 and the addition of two factors is equal to the coefficient of x, that is +9.įactor the given quadratic equation using +2 and +7 and solve for x.ĭecompose the constant term +14 into two factors such that the product of the two factors is equal to +14 and the addition of two factors is equal to the coefficient of x, that is -9.įactor the given quadratic equation using -2 and -7 and solve for x.ĭecompose the constant term -15 into two factors such that the product of the two factors is equal to -15 and the addition of two factors is equal to the coefficient of x, that is +2.įactor the given quadratic equation using +5 and -3 and solve for x.ĭecompose the constant term -15 into two factors such that the product of the two factors is equal to -15 and the addition of two factors is equal to the coefficient of x, that is -2.įactor the given quadratic equation using +3 and -5 and solve for x.
#Solving quadratic equations by factoring how to#
(iv) Write the remaining number along with x (This is explained in the following example). Examples of How to Solve Quadratic Equations using the Factoring Method What we need to do is simply set each factor equal to zero, and solve each equation for. (iii) Divide the two factors by the coefficient of x 2 and simplify as much as possible.

(ii) The product of the two factors must be equal to "ac" and the addition of two factors must be equal to the coefficient of x, that is "b". (i) In a quadratic equation in the form ax 2 + bx + c = 0, if the leading coefficient is not 1, we have to multiply the coefficient of x 2 and the constant term. This one right over here, you could almost do this in your head, it was nice and simple. So these are the possible solutions, and this is pretty neat. Divide both sides by two, and you get X is equal to 5/2. Solving Quadratic Equations by Factoring when Leading Coefficient is not 1 - Procedure Divide both sides by two, and we get X is equal to 3/2, or over here if we add three to both sides, we get two X is equal to five. If you need to learn or reinforce the techniques for factoring quadratic equations, you can visit our article: Factoring Quadratic Equations.Positive sign for smaller factor and negative sign for larger factor. To achieve this, we have to find two factors, which when multiplied, result in the original quadratic equation.įor example, the equation $latex x^2+2x-3=0$ can be factored in the form $latex (x+3)(x-2)=0$, since multiplying the factors gives us the original equation.
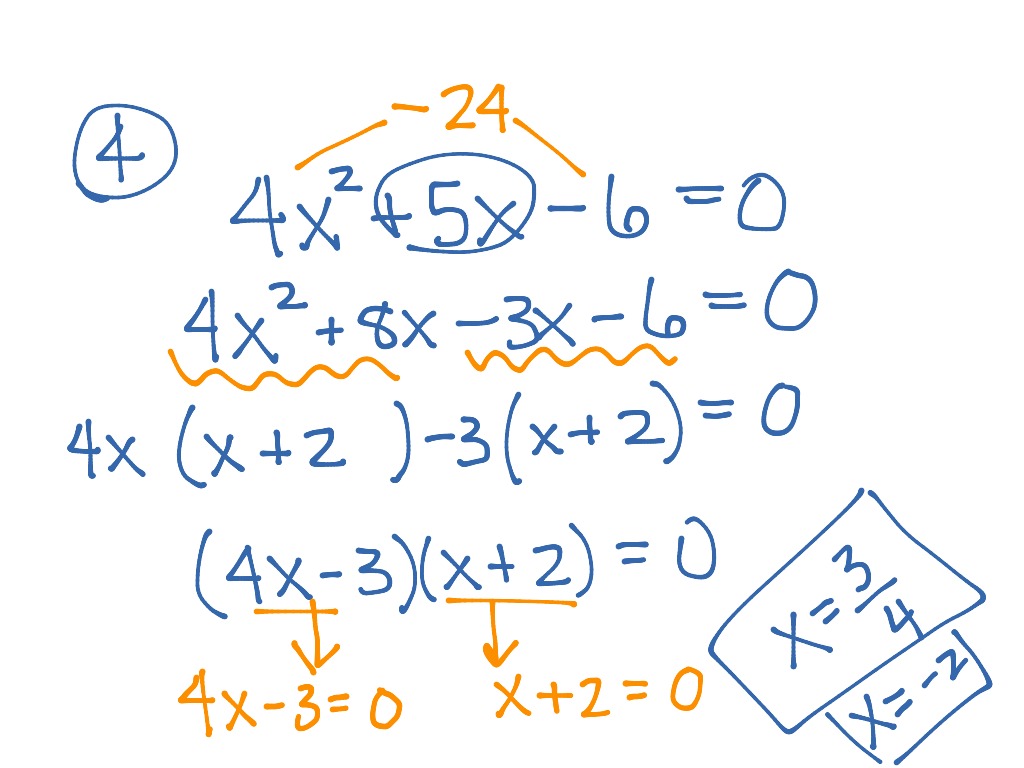
Recall that factoring a quadratic equation consists of writing an equation from the form $latex x^2+bx+c=0$ to the form $latex (x+p)(x+q)=0$. Step 4: Solve the equation for each factor. Solution to Question2 To factor the expression on the left, we need to write x 2 - 5 x + 6 in the form factored: so that the sum of a and b is -5 and their. Step 3: Form an equation with each factor by setting it equal to zero. This lesson plan includes the objectives, prerequisites, and exclusions of the lesson teaching students how to solve quadratic equations by factoring.

However, the method only works for the most basic equations. Step 2: Factor the quadratic equation using any method so that we can write it in the form $latex (x+p)(x+q)=0$. Lesson Plan: Solving Quadratic Equations: Factoring Mathematics 9th Grade. The example above shows that it is indeed easy to solve quadratics by factoring method. Step 1: Simplify and write the equation in the form $latex ax^2+bx+c=0$. To solve a quadratic equation by the factorization method, we have to follow the following steps: Solving Quadratic Equations by Factoring Date Period Solve each equation by factoring. How to solve quadratic equations by factoring?


 0 kommentar(er)
0 kommentar(er)
